Descrive le variazioni del tempo di individui in una popolazione, tramite modelli matematici, con scopi predittivi.
Esistono due modelli fondamentali.

modello esponenziale

e il modello logistico

Modelli di riproduzione

Esistono due modelli, estremi di un continuum, di tipologie riproduttive delle popolazioni.

• Riproduzione discreta
• Riproduzione continua

Dinamica di popolazione

Il modello più semplice per descrivere il cambiamento di una popolazione a livello di quantità tiene conto solo delle nascite e delle morti, non strutturato per età o taglia. Dove la riproduzione è continua.

N = No + B + D (+I - E)

Per la dinamica è importante che il conteggio sia in funzione del tempo, così che sia propriamente predittivo. In una popolazione chiusa (cioè senza fenomeni migratori)

Nt+1 - Nt = B - D

Crescita esponenziale

Considerando un cambiamento di popolazione in un tratto di tempo, e siccome le morti e le nascite assolute sono legate alla quantità di popolazione in quel momento, ne otteniamo anche rispettivamente il tasso di mortalità e il tasso di natalità

deltaN / deltat = (b-d)N

Così otteniamo il modello di crescita esponenziale.

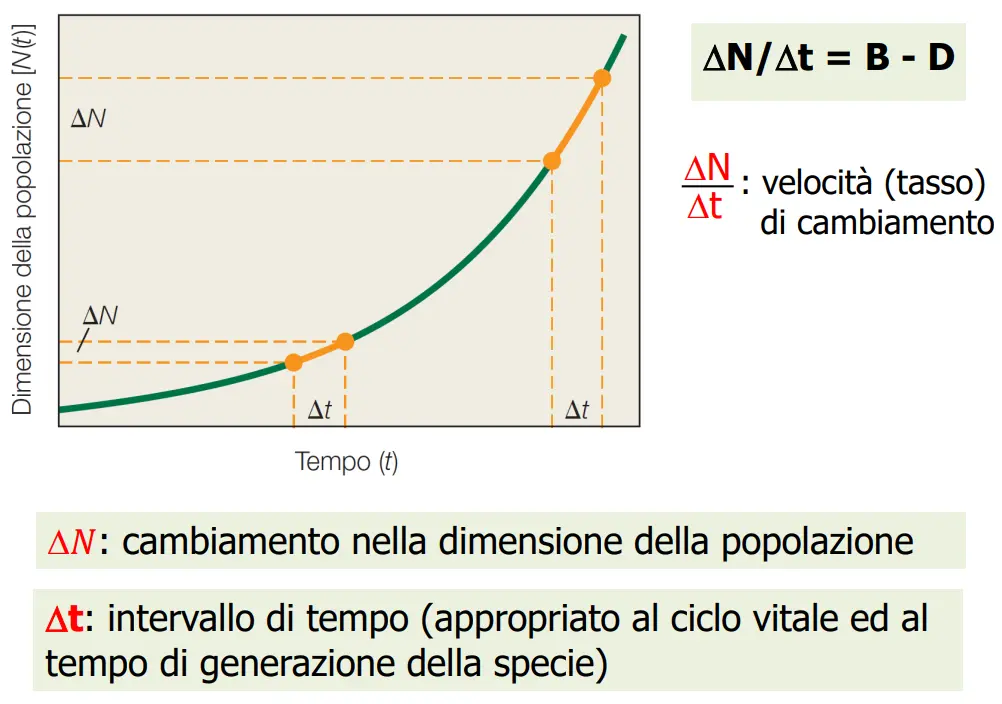
Derivando

E' altrettanto facile scrivere il modello attraverso la sua derivata, cioè quando t tende a 0. Così convertiamo i tassi in tassi intrinseci, per t che tende a 0.
Considerando r = tasso istantaneo di crescita, dove r = (b-d)

dN/dt = rN

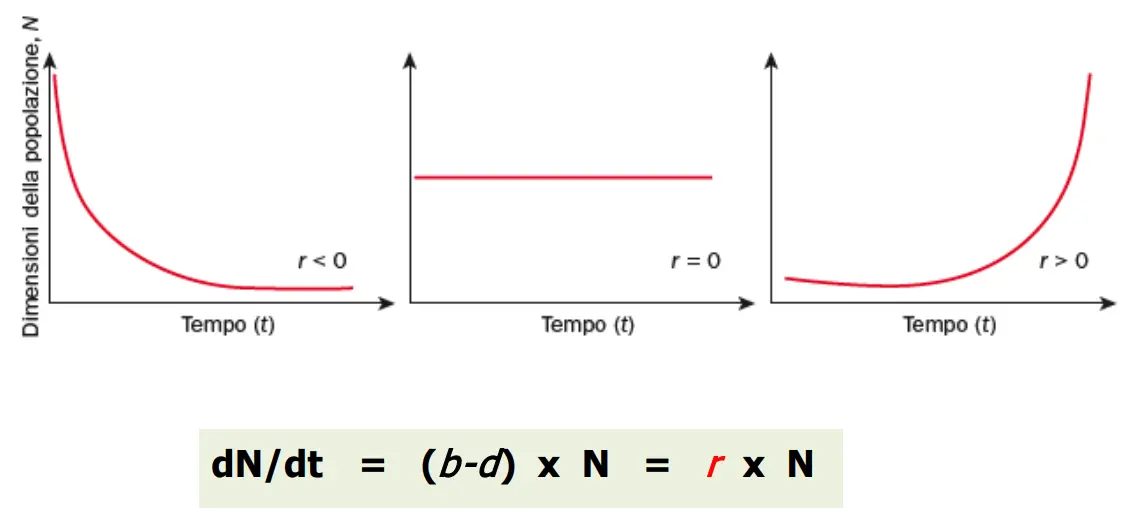
A seconda del valore di r, la popolazione cresce, decresce o è stabile (r=0)

Integrando

Integrando otteniamo una funzione per cui è facile fare predizioni sulle dimensioni della popolazione per ogni tempo t.

Nt = No x e^rt

Utilizzando una scala logaritmica, trasformo le curve esponenziali in rette, dove la pendenza diventa = r.

Considerazioni

• Modello deterministico
• Fattori stocastici non considerati
• Implicazioni per la conservazione
  • Se r<0, la popolazione cala fino all'estinzione

Nella realtà la crescita esponenziale è un modello che rappresenta popolazioni appena introdotte in un nuovo ambiente, dove le risorse non rappresentano un limite.

Crescita logistica

Dal libro
In realtà le risorse sono limitate, si instaura competizione intraspecifica.
L'aumento della popolazione implica un aumento della densità, e di conseguenza aumenta il tasso di mortalità e diminuisce il tasso di natalità. Quindi il tasso di crescita tende a 0 (dove b = d)

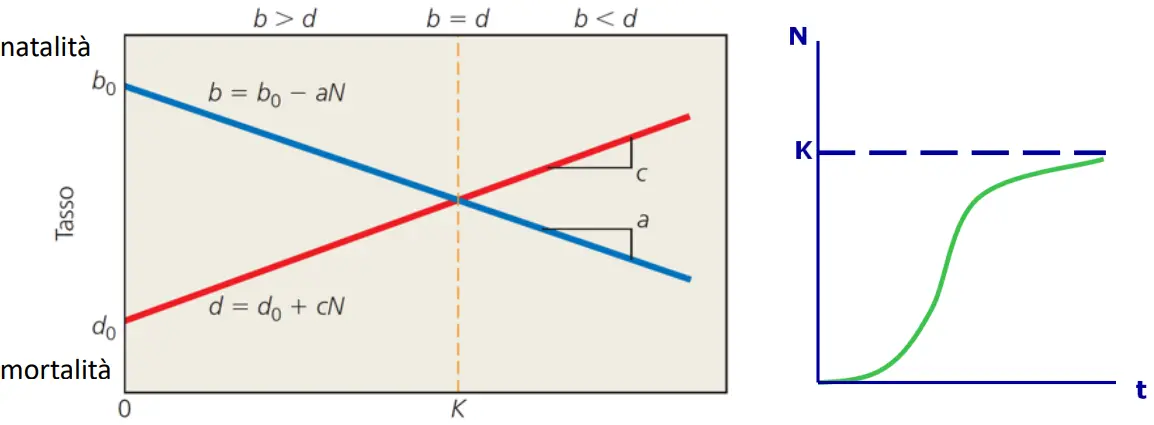
Capacità portante

Il punto in cui N = k, ovvero in cui b = d, dove l'ambiente raggiunge il numero massimo di individui che può sostenere è detto capacità portante.
Quando la popolazione è uguale a k, è in equilibrio col proprio ambiente
L'accrescimento è nullo.
All'equazione si aggiunge un termine che determina il rallentamento all'avvicinarsi a K.

In un ambiente limitato una popolazione inizialmente cresce esponenzialmente, poi raggiunge il limite di risorse e i tassi cambiano, arrivando a equivalersi.

dN/dt = rN x (K-N)/K

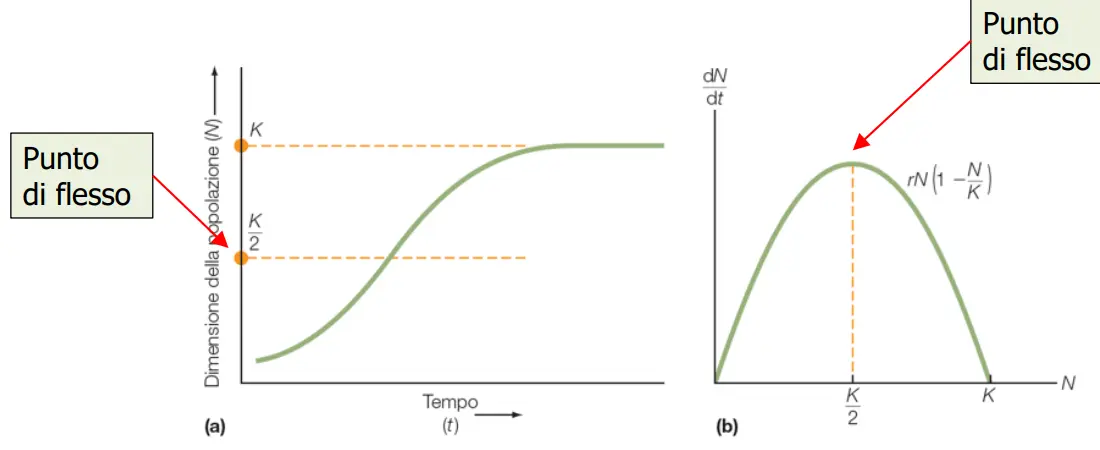
A ciò si aggiunge il punto di flesso (K/2), punto in cui la crescita decelera e non è più esponenziale. E' il punto in cui una popolazione può essere sfruttata al massimo, siccome r, il tasso di crescita, è massimo.

Meccanismi di regolazione densità dipendenti

All’aumentare della densità della popolazione, la disponibilità di risorse pro-capite diminuisce. Esiste quindi un feedback negativo (un controllo nel quale un cambiamento alla fine inibisce o inverte i processi che lo hanno determinato) tra aumento della popolazione e risorse ambientali disponibili.

I meccanismi di regolazione densità-dipendenti possono anche agire senza coinvolgere competizione, come malattie, parassiti, stress e cambiamenti ormonali o Predazione.

Crescita densità dipendente

Crescita densità-dipendente (calo del tasso di crescita individuale all’aumentare della densità).

Fecondità e mortalità densità dipendente

La fecondità densità-dipendente (calo della fecondità all’aumentare della densità) Fattori densità-dipendenti La fecondità è spesso legata alla crescita individuale (in lunghezza o peso), soprattutto in organismi con crescita indeterminata.

Mortalità densità-dipendente (aumento della mortalità all’aumentare della densità) Fattori densità-dipendenti Può provocare a sua volta una risposta nella crescita individuale, soprattutto in organismi con crescita indeterminata

Effetto Allee

Riduzione dei tassi di natalità e sopravvivenza in condizioni di bassa densità (è sempre un meccanismo densità-dipendente) In questo caso è coinvolto un feedback positivo.
Una popolazione che diminuisce non necessariamente aumenta la propria natalità

Ad esempio la difficoltà nel trovare partner e la minore collaborazione per le risorse

Esempio

Il declino (~ 90%) della popolazione tra il 1973 e il 2006 ha causato la diminuzione della densità nelle colonie e del numero delle colonie, con anche isolamento tra le colonie: - riduzione delle interazioni sociali - aumento del tempo impiegato nella vigilanza anti-predatoria - calo del tasso di nutrizione, sopravvivenza e riproduzione

Comportamento erratico

La dimensione della popolazione N fluttua attorno a K a causa della dinamicità delle popolazioni (nascite e morti) e ai ritardi nella risposta alla variazione della densità Comportamento erratico (non vuol dire «casuale») di N attorno a K.

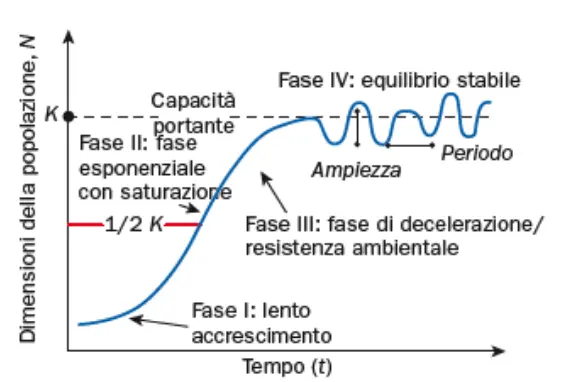
Inoltre la capacità portante non è fissa, ma essendo strettamente legata alle risorse ambientali è legata ai cambiamenti dell'ambiente.

Rischi per le popolazioni

Popolazioni piccole

Diversi meccanismi possono portare all'estinzione di una piccola popolazione

Ecologici:

• (effetto Allee)
  Ambientali
• Eventi casuali agenti sui tassi di natalità e mortalità
  Genetici
• Deriva genetica
• Inbreeding

Metapopolazioni

Una metapopolazione formata da tante piccole subpopolazioni corre un rischio minore di estinguersi

Tabelle di vita

A seconda dell'età dei membri / gruppi delle popolazioni, possono esserci distinti tassi di natalità o di mortalità per gli individui

Flashcards

Spiega il modello logistico
??
Il modello di crescita logistico tiene conto del limite che le risorse di un ambiente impone ad una popolazione. In natura non ci sono ecosistemi con risorse limitate, quindi le popolazioni incontreranno un plateau.

Quando una popolazione cresce esponenzialmente?
??
Quando il tasso di natalità è maggiore del tasso di mortalità. Ovvero quando r (il tasso intrinseco di crescita) è maggiore di 0.

Perchè in natura le popolazioni non possono crescere esponenzialmente in maniera indefinita?
??
Perchè l'ambiente pone un limite alle risorse disponibili ad una popolazione. Quando queste terminano di essere disponibili si instaura competizione intraspecifica e il tasso di mortalità arriva ad equivalere quello di natalità. Aumentà la densità della popolazione. Entra il concetto di capacità portante dell'ambiente.

Qual'è il modello più semplice che descrive la crescita di una popolazione?
??
Un modello semplice descrive solo i cambiamenti a livello di quantità, non strutturando per età o taglia. La riproduzione è continua.
N = No + B + D (+I - E)

Che considerazioni c'è da fare col modello di crescita esponenziale? In che contesti si applica nella realtà?
??
è fondamentalmente un modello deterministico

• Fattori stocastici non considerati
• Implicazioni per la conservazione
  • Se r<0, la popolazione cala fino all'estinzione
    Nella realtà la crescita esponenziale è un modello che rappresenta popolazioni appena introdotte in un nuovo ambiente, dove le risorse non rappresentano un limite.

Cos'è la capacità portante?
??
E' il punto di massima abbondanza di una popolazione, l'ambiente non può sostenere un numero maggiore di individui. Quando le risorse diminuiscono e la densità di popolazione aumenta, si instaura competizione tra gli individui. Aumenta perciò il tasso di mortalità mentre diminuisce quello di natalità. Quando si equivalgono la crescita diventa = 0 e si raggiunge il valore di N per cui la popolazione non cresce. Questo valore è la capacità portante.

Qual è l'equazione del modello logistico?
??
Il modello logistico tiene conto del limite delle risorse disponibili.
Un termine descrive la crescita esponenziale, mentre l'altro pone il limite a questa crescita.
dN/dt = rN - (K-N)K

Cos'è il punto di flesso?
??
E' uguale a K/2. E' il punto in cui la crescita di una popolazione decelera e non è più esponenziale. E' il punto in cui una popolazione può essere sfruttata al massimo, siccome r, il tasso di crescita, è massimo.

Cos'è l'effetto Allee?
??
E' un meccanismo di regolazione densità dipendente. Prevede la riduzione dei tassi di natalità e sopravvivenza in condizioni di bassa densità. E' il caso di popolazioni dove, in caso di densità eccessivamente basse, si instaurano feedback positivi che però bloccano la crescita della popolazione, ad esempio una densità bassa porta all'impossibilità di incontrare partner sessuali.

Cosa sono i meccanismi di regolazione densità dipendenti?
??
Sono meccanismi che instaurano feedback negativi all'aumentare della densità di una popolazione, siccome le risorse pro-capite diminuiscono.
Possono agire senza coinvolgere competizione, come malattie, parassiti, stress e cambiamenti ormonali o Predazione.

Come è legata la fecondità ai meccanismi di regolazione densità dipendenti?
??
La fecondità densità-dipendente (calo della fecondità all’aumentare della densità)

La fecondità è spesso legata alla crescita individuale (in lunghezza o peso), soprattutto in organismi con crescita indeterminata. Se diminuisce la taglia siccome sono presenti meno risorse pro-capite, diminuirà anche la fecondità

Come è legata la mortalità ai meccanismi di regolazione densità dipendenti?
??
Mortalità densità-dipendente (aumento della mortalità all’aumentare della densità) Fattori densità-dipendenti Può provocare a sua volta una risposta nella crescita individuale, soprattutto in organismi con crescita indeterminata.

Cos'è una metapopolazione?
??
Una metapopolazione è un insieme di subpopolazioni, connesse tra loro tramite migrazioni, ma essenzialmente indipendenti.
All'aumentare delle subpopolazioni aumenta la resilienza della metapopolazione, siccome l'estinzione di una subpopolazione non comporta l'estinzione della specie.

Cos'è una tabella di vita?
??
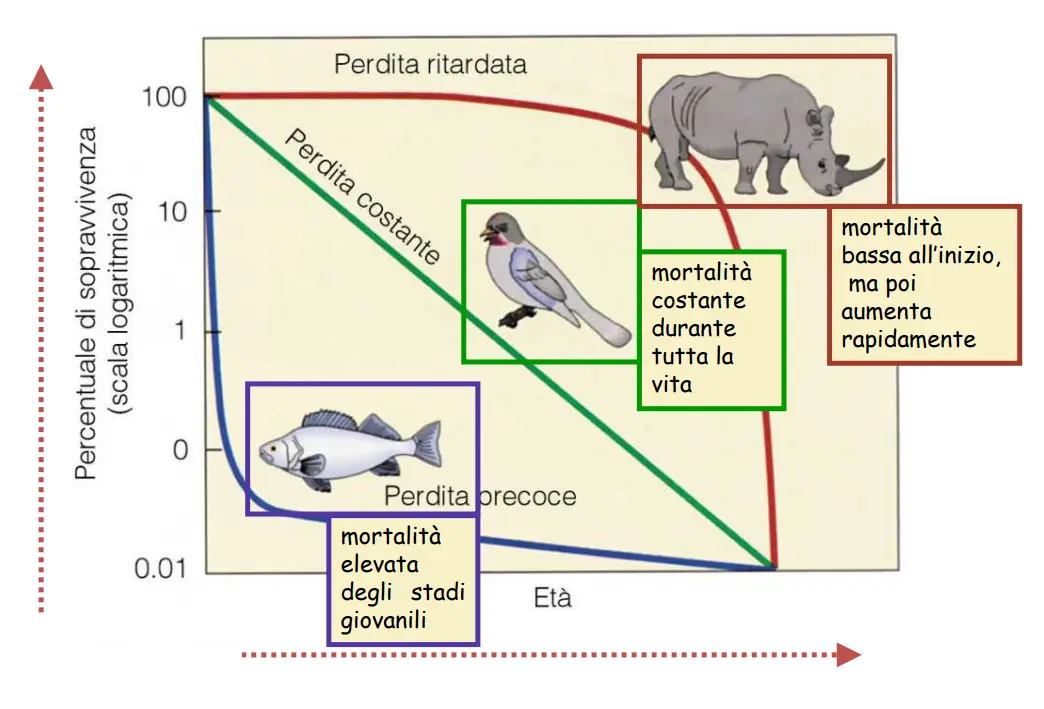
Modelli più complessi tengono conto delle differenze di taglia e di età all'interno di una popolazione e di come i tassi di mortalità sono distinti all'interno di queste classi. Da ciò derivano le curve di sopravvivenza.

#flashcards #review