237
The logistic model effectively has two components: the original exponential term (rN) and a second term (1 − N/K) that functions to reduce population growth as the population size approaches the carrying capacity. When the population density (N) is low relative to the carrying capacity (K), the term (1 − N/K) is close to 1.0, and population growth follows the exponential model (rN). However, as the population grows and N approaches K, the term (1 − N/K) approaches zero, slowing population growth. Should the population density exceed K, population growth becomes negative and population density declines toward carrying capacity.

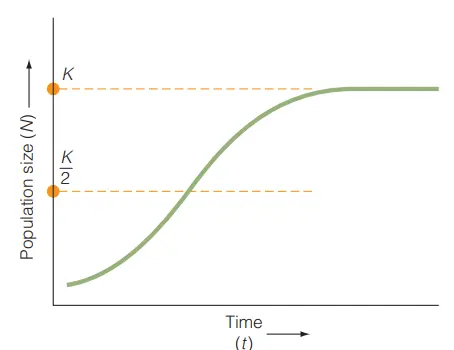
The graph of population size (N) through time for the logistic model is shown in Figure 11.2a. When the population is small, it increases rapidly but at a rate slightly lower than that predicted by the exponential model. The rate of population growth (dN/dt) is at its highest when N = K/2 (called the inflection point) and then decreases as it approaches the carrying capacity (K; Figure 11.2b). This is in contrast to the exponential model, in which the population growth rate increases linearly with population size.